
Use of this website constitutes acceptance of the Privacy Policy and User Agreement. Copyright © 2020 Kalimba Magic. All Rights Reserved.
“Just” intonation is tuning based on the notion that ratios of frequencies should be ratios of simple whole numbers. That is a complicated way of saying: the distance between notes in a scale should be simple. And it turns out the ear agrees: “just” intervals sound more pleasing than what your $20 digital tuner or your cell phone app will lead you to tune.
We’ll explain a simple way you can get most of the benefit of a just tuning.
Oh, and 432 Hz? We’ll talk about that too. While I understand 432 has some avid proponents, I myself do not perceive any musical or therapeutic benefit to a 432 Hz reference compared to a 440 Hz reference, but we’ll explain how to do that too.
First, the low hanging fruit. Most humans do not perceive absolute pitches, but most humans do perceive relative pitches. I cannot tell the difference between C and B and C# without context. Hearing one of these notes alone, I will not be able to tell whether it is one of three named notes, and if I try to start singing a C, I might very well start on a C#… or even a D on a particularly warmed-up day. But once I start singing and pick a reference note for my scale, I am very good at perceiving the relative distance between the notes.
People who can hear a note and say, “Oh, that is a C#” are said to have perfect pitch, and are about 1% of the population. They are mostly born with it, or develop it in their earliest years. The rest of us? We can learn the difference between C and D, or C and E – we discern the distance between two notes. We have what is called relative pitch.
I believe that relative pitch is more important for playing music than perfect pitch. I think most anyone can learn relative pitch.
Today, most music is tuned to a standard reference pitch of A 440 Hz, or 440 vibration cycles per second. All tuners come from the factory set up to do A 440. That is an absolute pitch. Why?
Before the 20th century, musical pitch was nonstandard. Every town in Europe had their own standard, to which the local musicians would all tune. Traveling musicians had to adapt their instruments’ tunings to the local standard so they would sound good. This was a huge hassle.
In a world where people tune kalimbas in Africa, send them to me, and I then send them to almost any country in the world, a standard tuning is obviously essential, and 440 Hz = A is as good a standard as any. I would have been OK with A 432, except, the whole world has already decided.
Or has it?
When you buy an electronic tuner, it likely has a “Calibration” feature. This permits you to change the reference pitch, from A 440 Hz to… 439, 438, 437… mine goes all the way down to 410 Hz. Or up as high as 470 Hz. So if I ended up in a village where everyone tuned to 457 Hz, I could calibrate my tuner to that higher reference pitch.
Or, if I were playing my hammered dulcimer for the first time in six months, and the entire instrument had gone sharp (increased humidity results in the wood absorbing more water, resulting in the wood expanding, stretching the strings and increasing the tension, which will make the whole instrument go sharp), I could determine the new mean pitch of the instrument and calibrate my tuner to that new pitch.
Or, people could band together and decide they liked the sound of music played on the 432 Hz tuning reference better than the 440 Hz reference.
One year ago, I played with such people, and I had to tune my guitar and kalimba down to A 432 Hz.
It is easy to do. Hit the tuner’s calibration button until 432 Hz appears in the upper left hand corner of the display, and then tune as you normally do, adjusting the pitch of your note up and down until the tuner registers that note is in tune. Voila! Done!
While 432 Hz is about a particular absolute tuning, it says nothing about the system of tuning within that reference frame. “Just intonation” is an entire system of how to define the relative pitches within a scale.
What? Haven’t people figured out the system of intonation by now? Well, they have – the equal temperment 12 tone system dominates music today… but the raw perfect harmonies don’t fit perfectly into that system.
The system of just intonation can be used with a 440 Hz reference, a 432 Hz reference, or any other reference pitch.
Just intonation in the 3rd, the 4th, the 5th, and the 6th intervals happens quite naturally. When two people are singing, or two violins are playing well together, they can be perfectly in tune with each other – even better than two notes that are supposedly perfectly in tune according to an electronic tuner. People have probably been singing just-intuned intervals for tens of thousandsof years. Yes, I assert ancient humans really were that sophisticated.
Before we get too far into just intonation, let me describe what your electronic tuner is trying to push on you: equal temperment. Equal temperment, in the 12-tone system that Western music occupies, means every half step interval has a ratio of frequencies equal to 2^(1/12) (two raised to the 1/12 power) = 1.059463… I’ll call this number p.
To go from A 440 Hz to Bb a half step up, multiply 440.00 Hz by p = 466.16 Hz. To go from A 440 Hz to B, a whole step up, multiply by p twice, or p^2 = 493.88 Hz. To go from A down to A flat, divide 440 Hz by p to get 415.30 Hz.
Incidentally, lets go back and look at 432 Hz. A half step around A is equal to a difference of about 24.7 Hz. If you tune to A = 432 Hz, down 8 Hz from A 440 Hz, that will be 8 Hz / 24.70 Hz – or about 1/3 of a half step flat from A 440.
Important note: your tuner will indicate the closest note to what it hears, and also the needle will indicate if that note is flat or sharp. When the needle is all the way to the left, you are 50 cents flat, or -50 cents. If the note got just a little bit flatter, it would register as the next lower note, but the needle would indicate that lower note is now 50 cents sharp. In other words, the range of needle, from -50 to +50, is 100 cents. That is, there are 100 cents in a half step. And the needle’s scale on my tuner is marked with dots every 5 cents and bigger dots every 10 cents.
You need to know what key your kalimba is in, and which tine maps to “Do” or “1”, which to “Re” or “2”, which to “Mi” or :3″, etc.
The table below shows you how you need to tune to get just intonation on a diatonic instrument. You will tune the “Do” note – G for example on the Alto kalimba – right exactly in tune acording to electronic tuner. That is what the “0” under the delta (triangle) means in the first row.
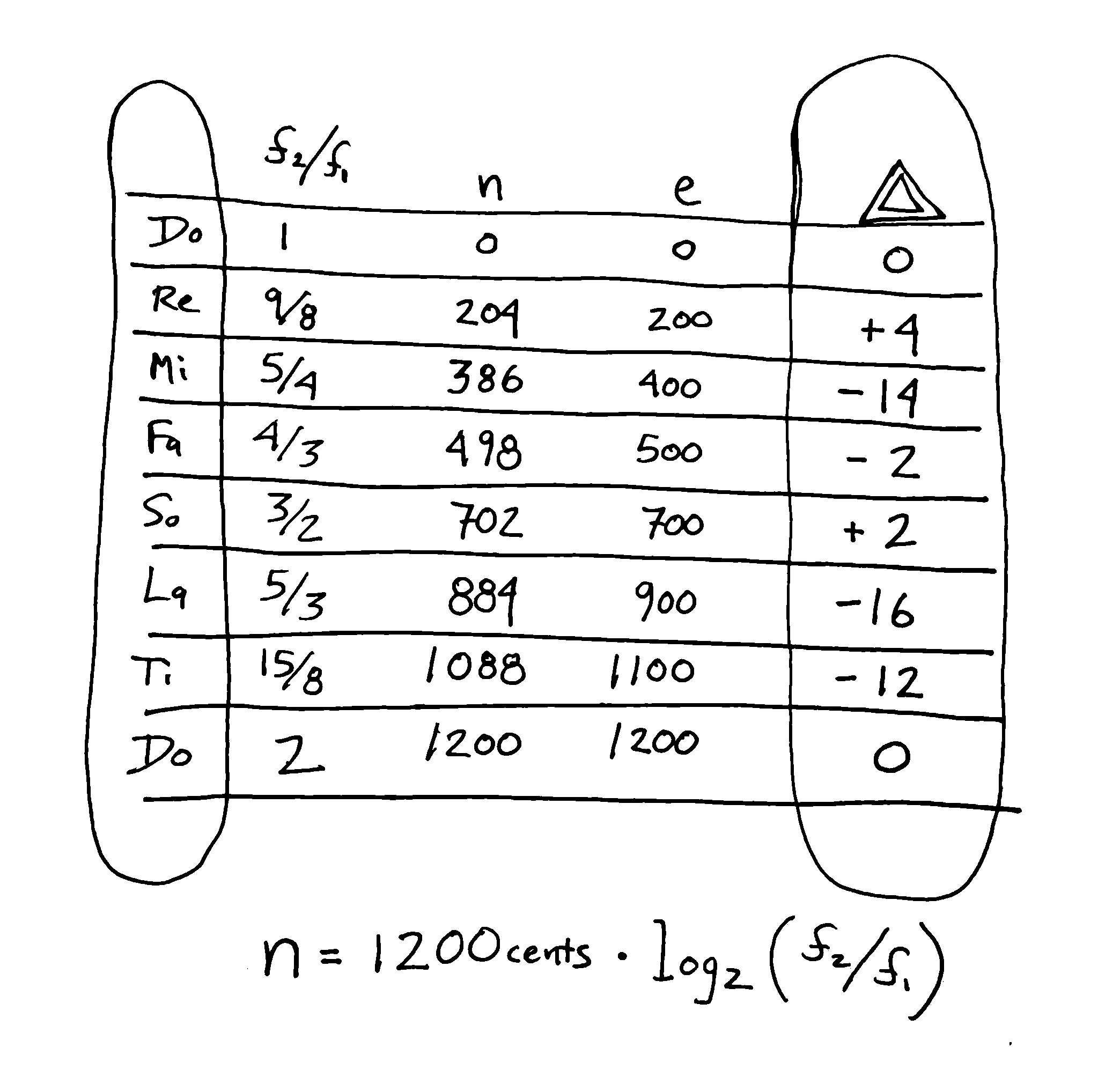
In this table, we indicate the just intonation frequency ratio with respect to Do, “n”, the cents above Do for just intonation, “e”, the cents above Do for equal temperment, and “Delta”, the number of cents flat or sharp of equal temperment required to tune that interval to just intonation.
Look at the third row, for “Mi” – the 3rd of the scale. A just 3rd should be tuned 14 cents lower that the equal temperment the tuner spits out. And it just so happens that my tuner – and probably your tuner too – has a little mark right at 14 cents flat. This makes it so easy!

The tuner above is registering my “B” note is about 14 cents flat – that is, perfectly tuned to a just 3rd in the kay of G.
You might be wondering: just how accurately can one tune? I think I can tune to about 2 cents RMS when tuning carefully. This limit is due, I think, to the natural jitteriness of the kalimba – tuner system, another way of saying the needle jumps around a bit when you are tuning the kalimba.
So, when we tune the 4th, Fa, and the 5th, So, which are supposed to be 2 cents flat and sharp respectively, we might not really be able to accomplish that – those small deltas are “lost in the noise” you might say.
But the just 6th, or “La”, should be tuned 16 cents flat – just a little bit to the left of the triangle at -14 cents. And the just 7th, at 12 cents flat, is a bit to the right of that triangle.
If you are an astute observer, you will notice there is also a black triangle near +20 cents. That is to tune a just minor 3rd, which is 16 cents sharp from the equal tempered interval.
Let me spell out what just went down – you can get most of the benefit of just intonation – that is, clearer more perfect harmonies – by tuning everything exactly as your tuner says… except tune the 3rd, the 6th, and the 7th a bit flat, right about where the -14 cent triangle is to the left of “0” on your tuner.
If you want your kalimba tuned to Just Intonation, or to the A = 432 Hz reference pitch, or both, just talk to us about it.
To hear a just intonation demonstration, click play on the media player below.


Sign up for our newsletter and free resources with your email address:
We pinky promise not to spam you and to only send good stuff.
 Assist Paul Tracey Rebuild His House in Pacific Palisades
Assist Paul Tracey Rebuild His House in Pacific Palisades 8-Note Spiral Kalimba Turned into a Student Karimba
8-Note Spiral Kalimba Turned into a Student Karimba Seek to Infuse Your Musical Moments With Beauty and Magic
Seek to Infuse Your Musical Moments With Beauty and MagicUse of this website constitutes acceptance of the Privacy Policy and User Agreement. Copyright © 2020 Kalimba Magic. All Rights Reserved.